借top K题目思考总结堆（heap）与优先队列（priority_queque）用法

一、前言

今天做了传说中的top K ，即“用大顶堆/小顶堆对数据进行排序”的经典题目

本题思路：

1. 用map记录每个元素出现的频率
2. 用heap对map进行排序并节选出前K个元素

若第一次见此类题，难点当为heap的原理和对应stl容器（priority_queue）的用法。查阅了一些资料，发现不管是leetcode题解抑或博客文章都写得略语焉不详，对新手不甚友好，故笔者试图用自己的话对其原理进行粗糙解释。

---

二、堆（heap）的原理和用法（下述所有例子默认用小顶堆）

1.定义

（1） 堆是一种具有特殊排序关系的完全二叉树，也就是说，堆首先得具有完全二叉树的所有特性
（2） 特殊排序关系指——以小顶堆为例——每个节点的value都小于其两个子节点 ；大顶堆反之

下图就是一个典型的小顶堆

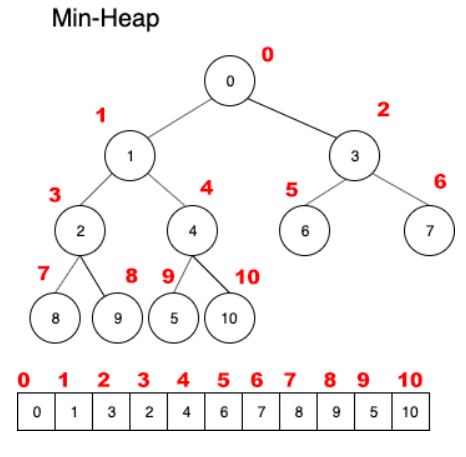
3.堆的建立（push）

对于一个已经建好的堆，push新元素的方法是：

1. 插入：将该元素插入到heap的尾部
2. 比较：然后不断“上浮”，直至满足堆的条件。所谓“上浮”，就是将该元素与其父节点进行比较，比父节点小则上浮一层，否则不动，一直操作直至上浮不动。

而若是要从零开始建立一个堆捏？很简单，从第一个元素开始，对每个元素都执行一次push操作就行了。
下图展示了从零开始建立一个heap过程

2.堆的删除（pop）

三步走：

1. 弹出：将堆顶元素（即最小的那个元素）直接pop
2. 提上：将heap的最后一个元素提到堆顶
3. 下沉：将提上的这个堆顶元素不断与其子节点比较，大于子节点就下沉一层，直至全满足定义

如下图所示

---

三、优先队列（priority_queue）的使用

1.定义

我们可以用c++ stl中的priority_queue容器来实现heap的操作，其定义如下

template<
    class T,
    class Container = std::vector<T>,
    class Compare = std::less<typename Container::value_type>
> class priority_queue;

T是指堆中元素的数据类型；
container指用于存储这些元素的底层容器类型（默认用vector，一般也不用改）；
compare是元素之间的比较方式，用于决定建立的是大顶堆or小顶堆，默认用less函数建立大顶堆（当然，你也可以自定义compare方法来建立一些奇奇怪怪的堆。。）

2.常用方法

和普通队列一样，常用的就pop()、push()、top()、empty()

3.代码示例

#include <functional>
#include <queue>
#include <vector>
#include <iostream>
 
template<typename T> void print_queue(T& q) {
    while(!q.empty()) {
        std::cout << q.top() << " ";
        q.pop();
    }
    std::cout << '\n';
}
 
int main() {
    std::priority_queue<int> q;
 
    for(int n : {4,1,2,5,3})
        q.push(n);
 
    print_queue(q);
 
    std::priority_queue<int, std::vector<int>, std::greater<int> > q2;
 
    for(int n : {4,1,2,5,3})
        q2.push(n);
 
    print_queue(q2);
 
    // 用 lambda 比较元素。
    auto cmp = [](int left, int right) { return (left ^ 1) < (right ^ 1); };
    std::priority_queue<int, std::vector<int>, decltype(cmp)> q3(cmp);
 
    for(int n : {4,1,2,5,3})
        q3.push(n);
 
    print_queue(q3);
 
}

运行结果：

上述代码及运行结果，与前面我手画的那两张图都是吻合的

---

四、题解

回到开头那道topK力扣题，答案如下

class Solution {
public:
    // 小顶堆
    class mycomparison 
    {
        public:
            bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) 
            {
                return lhs.second > rhs.second;
            }
    };

    vector<int> topKFrequent(vector<int>& nums, int k) {

        unordered_map<int, int> map; 
        for (auto iter : nums) {
            map[iter]++;
        }

        // 对频率排序
        // 定义一个小顶堆，大小为k
        priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;

        // 用固定大小为k的小顶堆，扫面所有频率的数值
        for (auto it = map.begin(); it != map.end(); it++) 
        {
            pri_que.push(*it);
            if (pri_que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
                pri_que.pop();
            }
        }

        // 找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒序来输出到数组
        vector<int> result(k);
        for (int i = k - 1; i >= 0; i--) {
            result[i] = pri_que.top().first;
            pri_que.pop();
        }
        return result;
    }
};

做一些解释说明：

1. 首先注意，我们要找出前K大的元素，那要用的是小顶堆，因为小顶堆才能把小元素排出去，剩下的就是前K大元素嘛

2. map中的单个元素的数据类型是pair<Type, Type>

3. 关于compare方法的理解：默认的less方法建立的是大顶堆，要建立小顶堆则改用greater<T>

   然后所谓的less方法，是将第一个实参（称之为左实参）与第二个实参（称之为右实参）进行比较，return left<right——那么左实参更小时则为true，为true则交换；greater方法反之，return left>right；

   在上述代码的自定义方法mycomparison中也可以说明这一点，它使用的是return left>right,即greater方法，即建立小顶堆

总结：
建立大顶堆 = less方法 = return left < right
建立小顶堆 = greater方法 = return left > right

TO-DO：
上述第三条纯属自己理解，这么死记用来做题应用没啥问题，但还是得挑个良辰吉日去翻翻源码才行捏😣