EE364A笔记
《EE364A笔记》
Lecture_1 Introduction
- 最小二乘问题
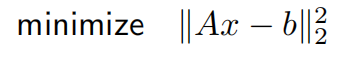
- 有解析解:$x^*=(A^TA)^{-1}A^Tb$
- 现已有成熟方法和软件来解决最小二乘问题
- 线性规划问题
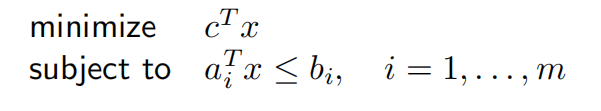
- 没有解析解
- 现已有成熟方法和软件来解决线性规划问题
- 凸优化问题
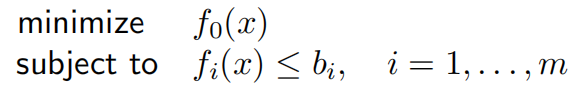
其中目标函数 f0 和约束函数 fi 都是凸的,即满足:
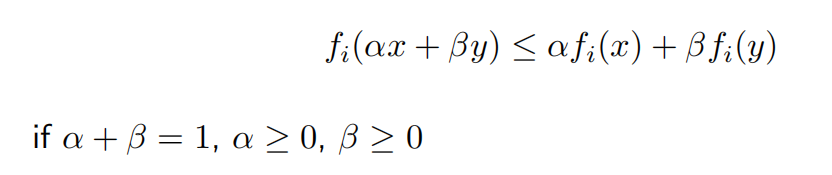
Lecture_2 Convex sets
一、凸包与凸集
二、如何保证一个集合C的凸性
- 使用定义
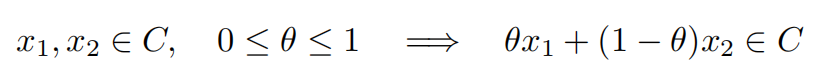
- 证明C是由简单凸集经过以下操作得到:
-
**相交:**任意个数的凸集相交仍为凸集
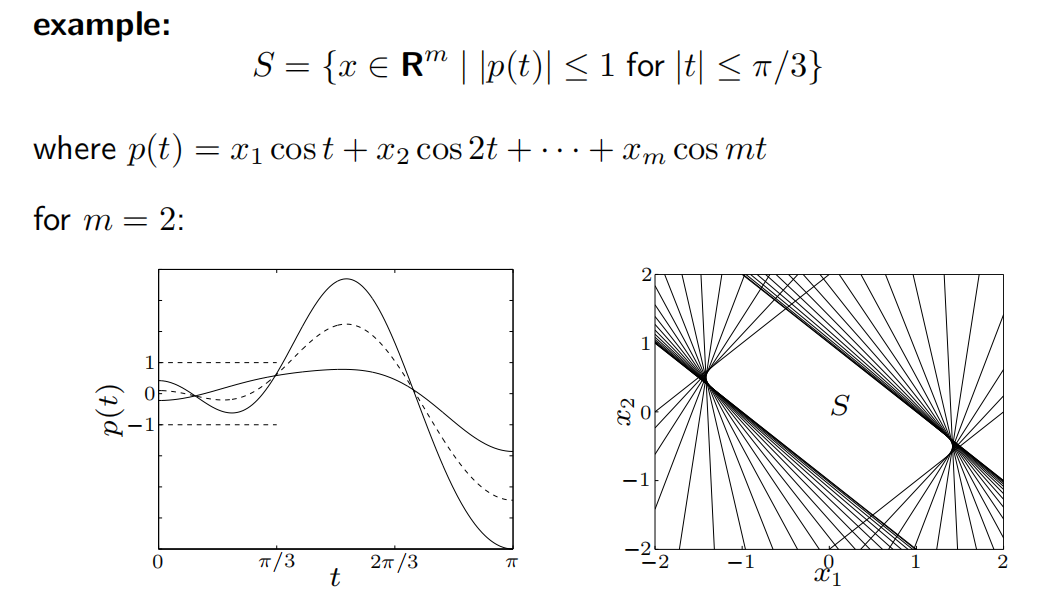
为什么说S是凸集捏?
首先cos是偶函数,所以 t 的范围简化为0到pi/3,我们假设 t 为该范围中的某个定值;
定义子集$S_t={ x\in R^m | \left\vert p(t)\right\vert \le1 }$,即先固定 t ,
则此时$\left\vert p(t)\right\vert \le1$是两个半平面的交集(因为 p(t)是[cos t, cos 2t]和[x1, x2]的内积,$p(t) \le1$是个半平面, $p(t) \ge -1$也是个半平面 ),所以 St 为凸集
而$S=\cap S_t ,t\in(0,\pi/3)$,即为无数个凸集的交集,故 S 仍未凸集(见上右图)
- **仿射函数:**凸集经仿射变换(缩放、平移、投影)仍是凸集
- 透视函数与线性分式函数
透视函数P:$R^{n+1}\rightarrow R^n$
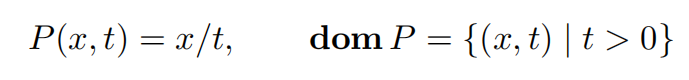
线性分式函数 f:$R^{n}\rightarrow R^m$
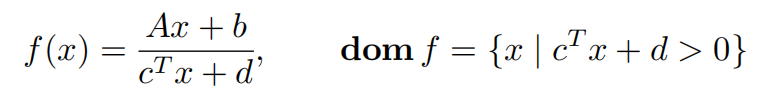
三、支撑超平面定理
如果C是凸集,那么在其每一个边界点上都存在至少一个支撑超平面(几何意义是切线、切面)
💡 PS. 支撑超平面不一定唯一,如矩形顶点处就有无数个超平面(因为边界突变)
Lecture_3 Convex functions
-
常见凸函数
-
指数函数
-
幂函数:$x^\alpha,\alpha \ge1,or ,\alpha\le0$
-
熵函数:$xlogx$
-
所有的范数
-
-
拓展函数

- 上境图(epigraph)
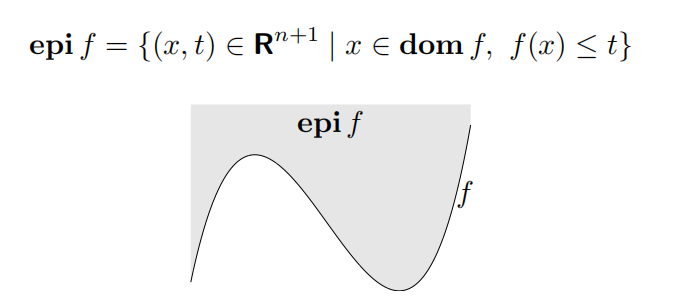
f 为凸函数 $\iff$ 的上境图为凸集
-
共轭函数
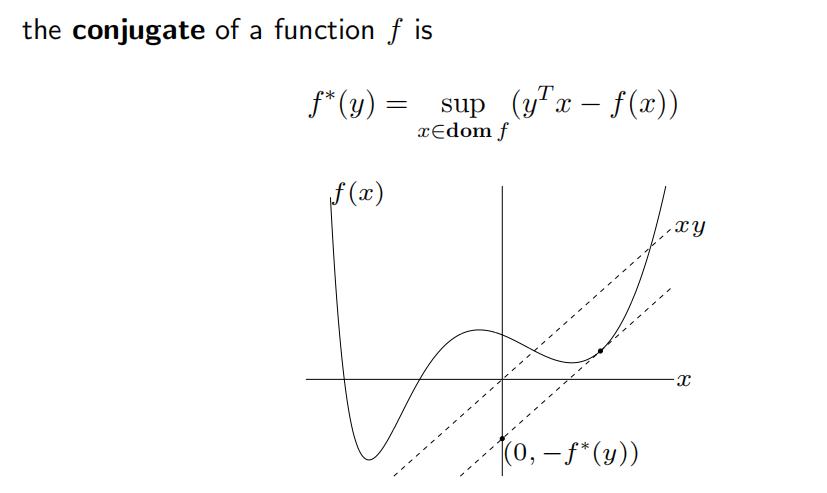
$f^*$始终是凸函数(即使 f 不凸)
举例:
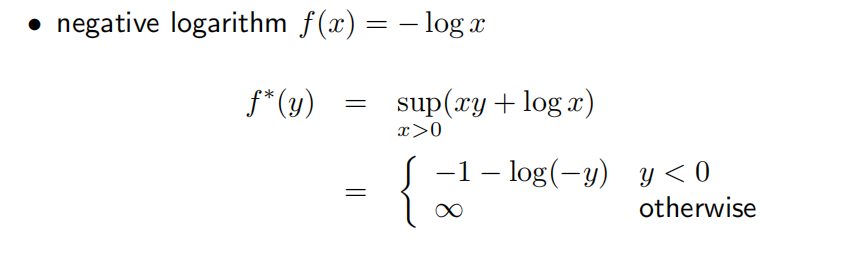
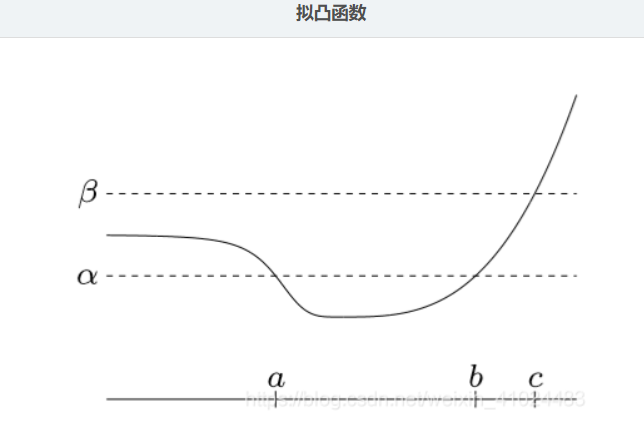
- 拟凸函数(quasiconvex function)
定义:若 dom f 为凸集,且对任意的 α ,其下水平集
$$
S_\alpha={x\in domf | f(x) \le \alpha }
$$
Lecture_4 Convex optimization problems
- 标准形式
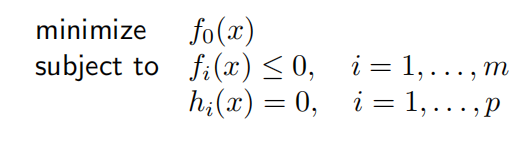
- 凸优化问题
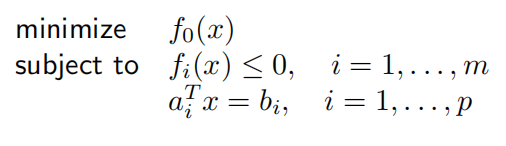
其中 fi(x) 都是凸的;等式约束是仿射的
💡 PS. 凸优化问题的任何局部最优解都是全局最优解
-
一些常见的转换技巧
- 消除等式约束

即先把 Ax=b 解出来,再带到不等式约束中
- 引入等式约束
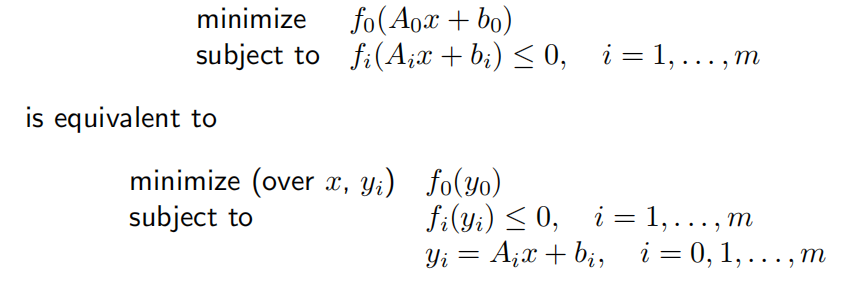
- 引入松弛变量
-
线性规划问题(Linear Program, LP)
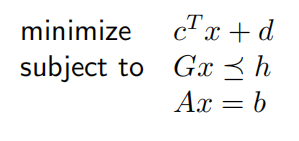
几何解释为,线性规划的可行域是多面体P,该最优问题就是要在P上求仿射函数$c^Tx+d$的极小值
举例:
一份健康的饮食包含m种不同的营养,每种至少需要b1,…,bm。我们可以从n种食物中选择非负的量x1,… , xn以构成一份食谱。单位第 j 种食品含有营养 i 的量为 aj,而价格为 cj。我们希望设计出一份最便宜的满足营 养需求的食谱。这一问题可以描述为线性规划
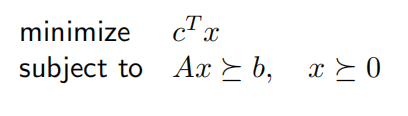
- 二次优化问题(Quadratic program,QP)
目标函数是凸二次型且约束函数为仿射
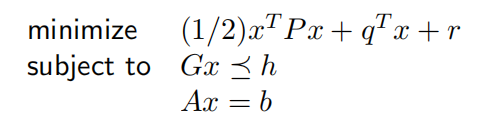
几何解释:可行集是多面体P,虚线为凸二次目标函数的等位线
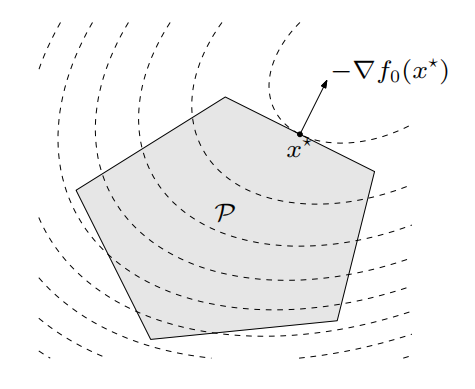
线性规划是二次规划的特例(P取0时退化为线性规划)
- 二次约束二次规划问题(QCQP)
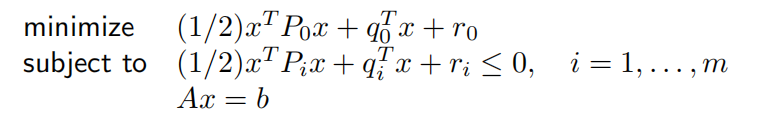
在二次规划的基础上,若不等式约束条件也是凸二次型,则称之为QCQP
- 二阶锥规划(Second order cone programming,SOCP)
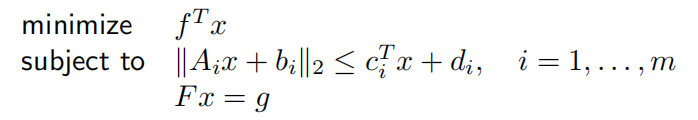
当 ci = 0时,退化为一个QCQP问题
Lecture_5 Duality
- Lagrange对偶函数
一个标准形式的问题(不要求是凸的)
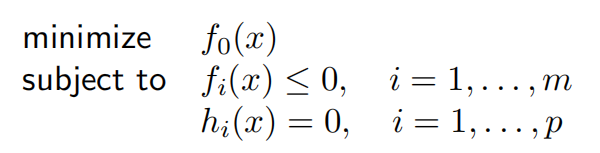
把它写成
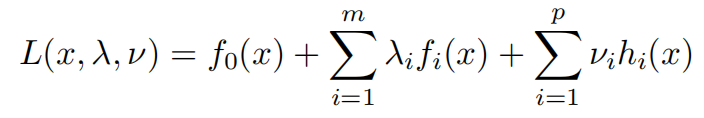
所谓的Lagrange对偶函数,就是去求它的下确界
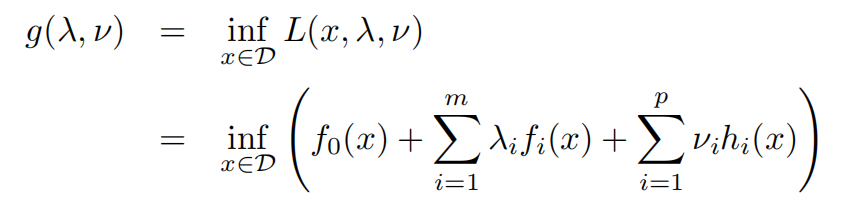
对于可行域内所有的$\tilde{x}$,皆有$p^* \ge g(\lambda,v)$,即$g(\lambda,v)$是原问题最优值的下界
- 举例:线性方程组的最小二乘解
考虑问题:
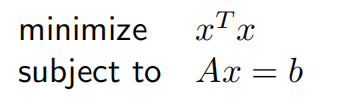
其Lagrange函数为:
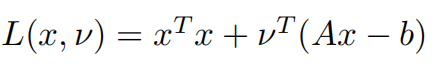
为得最小值,求其导数:
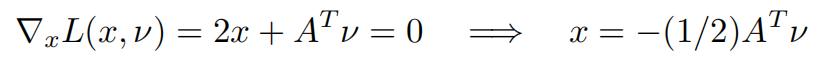
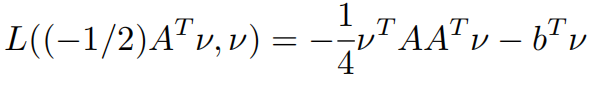
所以可得原问题最优解的下界为:
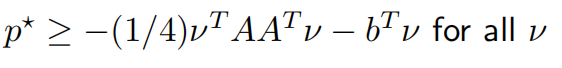
- Lagrange对偶问题
求Lagrange函数的最大值,也就是原问题的最好下界,这就是所谓的Lagrange对偶问题
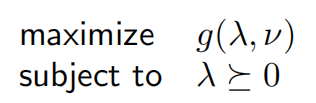
举例:
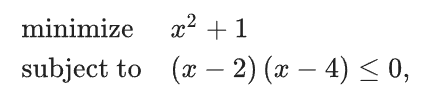
其Lagrange函数为:
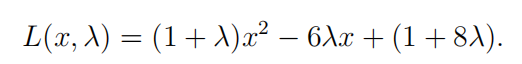
💡 PS. 注意:此时 x 的定义域是R,也就是说不用再去考虑 (x-2)(x-4)为负这个约束条件,因为Lagrange函数 本身就已经包含了这个条件
那么显而易见,对于这个以 λ 为自变量的二次函数,$\lambda \le -1$时下确界为 -∞ ;$\lambda > -1$时,在$\tilde{x}=3\lambda/(1+\lambda)$处取最小值,即
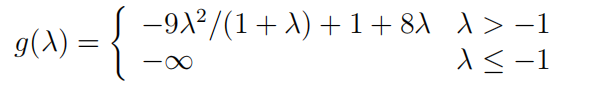
此时我们得到了所谓的Lagrange对偶问题:
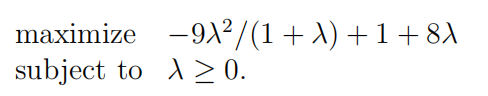
容易验证得到此时的最优点为 λ=2,最优值为5,和原问题一致(这是必然的,因为当 x 属于(2, 4)时不等式严 格成立,即满足Slater条件,且原问题是凸问题,那么强对偶性成立)
💡 PS. 除了Slater条件之外,还有其它很多判断准则
- 强弱对偶性
Lagrange对偶问题的最优值用$d^*$表示
- 弱对偶性指$d^* \le p^*$,弱对偶性始终满足(即使原问题不是凸的)
- 强对偶性指$d^* = p^*$,原问题是凸的时候通常(但不总是)满足强对偶性
- Slater约束准则
对于一个凸问题
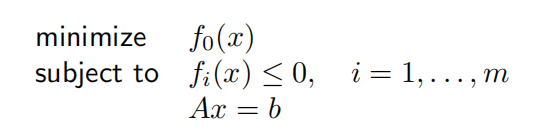
如果存在一个点$x \in intD$(内点),使得$f_i(x)<0, and,Ax=b$(即不等式约束严格成立),则称之为满足Slater约束,此时强对偶性成立
- 互补松弛性(Complementary slackness)
假设强对偶性成立,$x^$是原问题最优解,$(\lambda^,\nu^*)$是对偶问题的最优解
则有:
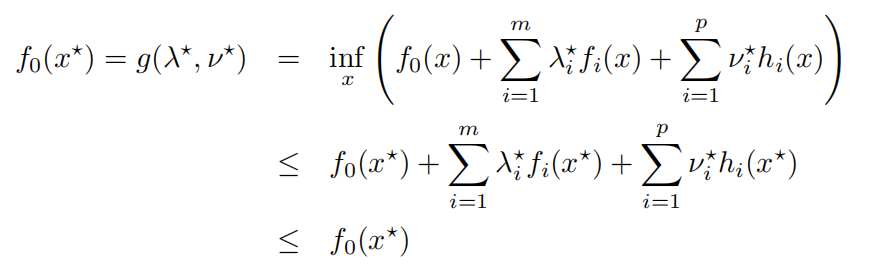
得到结论:
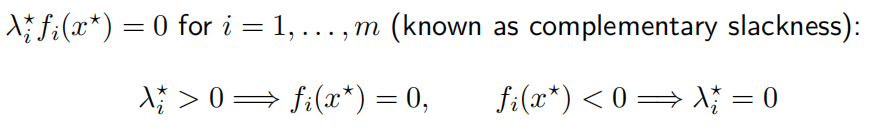
该结论就是所谓的互补松弛性
- KKT最优条件
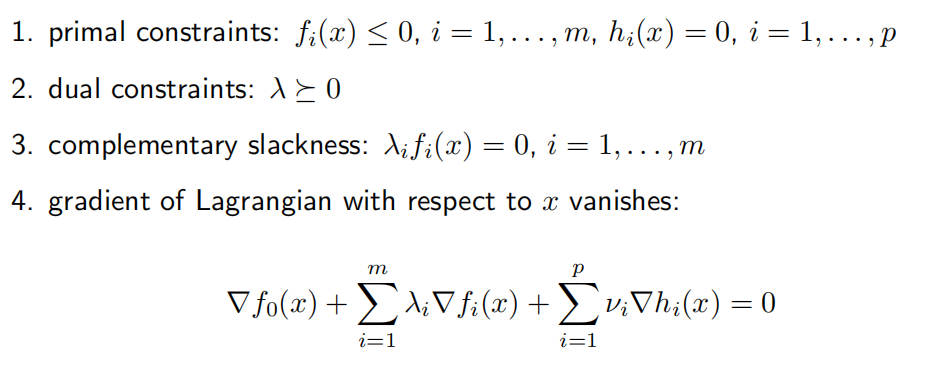
对于一个凸问题来说,若某组$(\tilde{x},\tilde{\lambda},\tilde{\nu})$满足KKT条件,那它们就是最优解
Lecture_6 Approximation and fitting
- 范数逼近
典型的范数逼近问题是具有以下形式的无约束问题:
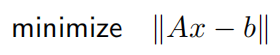
从逼近的角度进行解释:
通过将 Ax 表示为$Ax=x_1a_1+…+x_na_n$,其中 ai 为 A 的列,我们可以看出,范数逼近问题的目标是用 A 的列的线性组合,尽可能准确地逼近或拟合向量 b
- 最小二乘逼近
取范数为2,则原问题转换为:
$$
min ||Ax-b||_2^2
$$
将目标函数表示为凸二次函数:
$$
f(x)=x^TA^TAx-2b^TAx+b^Tb
$$
求其导数有:
$$
\nabla f(x)=2A^TAx-2A^Tb=0
$$
即 x 满足:
$$
A^TAx=A^Tb
$$
可得其唯一解$x=(A^TA)^{-1}A^Tb$
- 罚函数逼近
$l_p$范数逼近问题的目标函数为:
$$
(|r_1|^p+\cdots+|r_m|^p)^{1/p}
$$
其中 ri = Ax - b ,称之为残差,所谓的范数逼近,就是要残差尽可能地小,那么我们可以把范数逼近问题转换为以下形式:
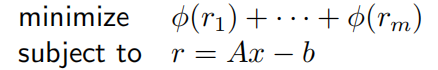
其中 Φ 称之为罚函数,我们通常将Φ设为一个对称的、非负的凸函数,则上述问题是一个凸优化问题
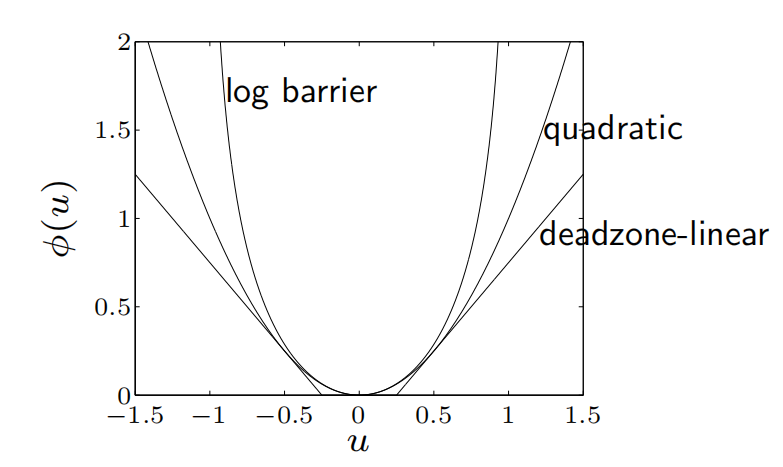
常见的罚函数:
-
二次罚函数$\phi(u)=u^{2}$
-
带死区的罚函数$\phi(u)=\max{0,|u|-a}$
-
对数罚函数
$$
\phi(u)=\begin{cases}-a^2\log(1-(u/a)^2)&|u|<a\ \infty&\text{otherwise}\end{cases}
$$
- 正则化逼近
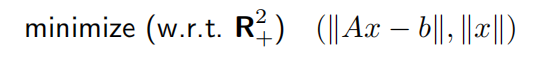
研究的是双目标优化问题,即同时让|Ax-b|和|x|尽可能地小,这在鲁棒逼近中可解释为:x 较小时Ax=b对误差的鲁棒性更好
-
信号重构问题
假设信号被加性噪声 v 污染,即
$$
x_{cor}=x+v
$$
所谓信号重构,就是在给定受污染信号 xcor 的情况下,构建对原始信号 x 的估计值 $\hat{x}$,也叫光滑化
重构问题的一个简单形式是双准则问题
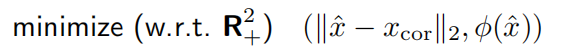
其中 Φ 是凸的,称为正则化函数或光滑目标。这个双准则问题,就是要寻求一个接近被污染信号并且光滑的 信号
- 二次光滑
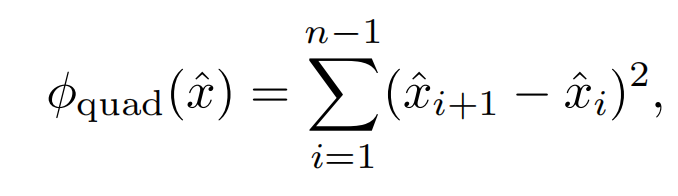
- 总变差重构
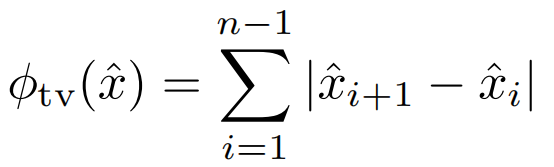
- 鲁棒逼近
问题形式为,在 A 不确定的情况下,最可能地最小化$||Ax-b||$
两种解决思路:
- 随机:假设 A 是随机的,最小化$E||Ax-b||$
- 最坏情况:求$min,sup||Ax-b||$
Lecture_10 Unconstrained minimization
- 定义
字面意思,没有约束条件的优化问题,我们假设 f 是可微凸函数,那么无约束优化问题其实就是去求梯度为零 的点

- 下降方法
即选择合适的搜索步长 t
- 精确直线搜索
找到让函数值最小的那个步长 t,即
$$
t=argmin_{s \ge 0}, f(x+s\Delta x)
$$
当目标函数形式简单,能求得解析解时可考虑使用这种方法
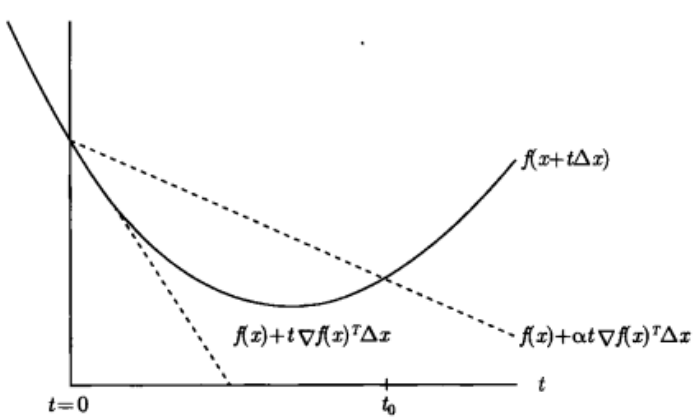
- 回溯直线搜索

基本思路是:先采用单位步长,若不满足条件,则不断缩小。
满足条件时的几何意义:$f(x+t\Delta x)$落入两条虚线之间的范围
- 其余内容参考《最优化计算方法(文再文)笔记》
Lecture_11 Equality constrained minimization
- 定义

x* 为最优点的充要条件是:存在 v* 满足
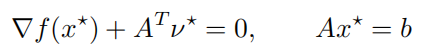
-
等式约束二次规划
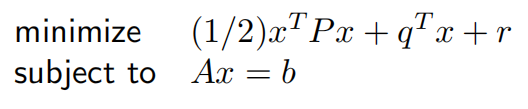
那么此时最优性条件为:
$$
Ax^=b, Px^+q+A^Tv^*=0
$$
写成矩阵形式为:
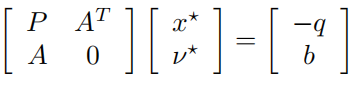
称之为等式约束优化问题的KKT条件
- 等式约束的Newton方法

**思路:**二阶taylor展开转换为
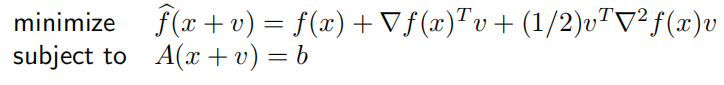
即KKT条件为
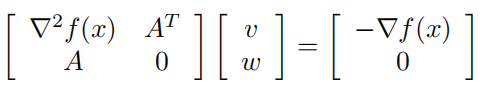
最后求解出来的那个$\Delta x_{nt}$就是newton方向,$x+\Delta x_{nt}$是对原问题真正的最优解 x* 的一个很 好的估计
另外,我们定义newton减量为:
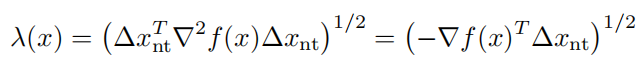
整个算法流程为:
