event-triggered系列论文学习

Paper 1：Event-Triggered Real-Time Scheduling of Stabilizing Control Tasks, 2007, TAC

一、motivation

​ 传统的固定时间周期的采样方式缺乏严格量化证明（时间周期为多少合适？少了不准确，多了浪费资源），而在微型处理器上又希望能尽可能节约计算资源， 所以考虑将周期采样转换为非周期采样，采样时间由某个“事件”来触发。

二、预备知识

1. $k$类函数、$k_\infty$类函数

​ 如果连续函数$\alpha:[0,a) \rightarrow [0,\infty)$严格递增，且$\alpha(0)=0$，则$\alpha$属于$k$类函数；更进一步地，如果$a=\infty$，当$r\rightarrow \infty$时，$\alpha®\rightarrow\infty$，那么$\alpha$属于$k_\infty$类函数

2. 问题描述

   控制系统：$\dot x=f(x,u)$

   反馈控制：$u=k(x)$

   恒定控制：$t\in[t_i+\Delta,t_{i+1}+\Delta]\Longrightarrow u(t)=u(t_i+\Delta)$（Δ是现实中的额外耗时，IO读取、计算耗时之类的）

   测量误差：$t\in[t_i+\Delta,t_{i+1}+\Delta]\Longrightarrow e(t)=x(t_i)-x(t)$

3. ISS Lyapunov函数

   

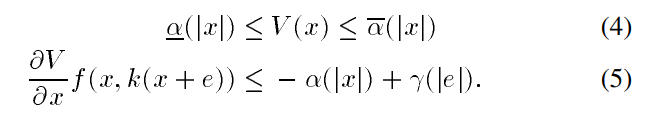
   其中$\underline\alpha,\alpha,\overline\alpha,\gamma$都是$k_\infty$类函数

三、event-triggered 机制

1. 如果我们设置有关误差的约束条件为：
   $$
   \gamma(|e|)\leq\sigma\alpha(|x|),\quad\sigma>0\quad\quad(8)
   $$
   将其代入公式 (5) 可得：
   $$
   \frac{\partial V}{\partial x}f(x,k(x+e))\leq(\sigma-1)\alpha(|x|)
   $$
   那么此时我们只需要让$\sigma<1$就可保证Lyapunov函数 V 是递减的。因此，我们可以将事件触发规则设置为下式：
   $$
   \gamma(|e|)=\sigma\alpha(|x|)\quad\quad(9)
   $$

2. 在设置好触发规则之后，一个相应的问题是：触发时间由 (9) 隐式定义，那如何保证两次触发时间不会无限接近，从而造成芝诺行为呢？

   原文通过Lipschitz条件证明了只要时延Δ足够小，则最小执行间隔时间存在，也就保证了$t_i-t_{i+1}$的下界，即$t_i-t_{i+1}\ge\tau,\tau\in\mathbb{R}^{+}$

   具体证明过程略

   

3. 仿真代码
   $$
   \left[\begin{matrix}\dot{x}_1\\
   \dot{x}_2\end{matrix}\right]=\left[\begin{matrix}0&1\\
   -2&3\end{matrix}\right]\left[\begin{matrix}x_1\\
   x_2\end{matrix}\right]+\left[\begin{matrix}0\\
   1\end{matrix}\right]u
   $$

   $$
   V=x^TPx
   $$

   $$
   \begin{aligned}\partial V/\partial x(Ax+BKx)=-x^{T}Qx\end{aligned}
   $$

   $$
   P=\left[\begin{array}{cc}1&\frac{1}{4}\\
   \frac{1}{4}&1\end{array}\right],\quad Q=\left[\begin{array}{cc}\frac{1}{2}&\frac{1}{4}\\
   \frac{1}{4}&\frac{3}{2}\end{array}\right]
   $$

   把测量误差带入表达式，我们有：
   $$
   \frac{\partial V}{\partial x}\Big(Ax+BKx+BKe\Big)\leq-a|x|^2+b|e|x|
   $$
   其中
   $$
   a=\lambda_m(Q)>0.44\quad b=|K^TB^TP+PBK|=8
   $$
   $\lambda_m(Q)$表示 Q 的最小特征值，$\sigma b$应比0.44更小，算出来$\sigma$的上界约为0.05，我们可以取$\sigma’=0.03$

   % Tabuada, P. (2007). 
   % Event-triggered real-time scheduling of stabilizing control tasks.
   % IEEE Transactions on Automatic Control,52(9), 1680-1685.
   
   
   clc;        
   clear;      
   close all;
   
   %% system define
   A = [0 1; -2 3];
   B = [0; 1];
   K = [1 -4];
   P = [1 0.25; 0.25 1 ];
   Q = [0.5 0.25; 0.25 1.5];
   x0 = [0.5 0.5]';
   dt = 0.001;
   trigger_count = 0;
   
   % sigma是上界，sigma_prime应小于sigma
   % 原论文中有解释
   sigma_prime = 0.03;
   sigma = 0.05;
   
   %% simulation
   x_buffer = [];
   u_buffer = [];
   error_buffer = [];
   error_trigger = [];
   error_upper_bound = [];
   
   x = x0;         
   u = K*x0;    
   syms s
   
   % 定常连续系统方程的离散化
   % 具体计算原理可参考https://zhuanlan.zhihu.com/p/556915351的2.2节
   Ad = expm(A*dt);
   Bd = int(expm(A*s),0,dt)*B;
   Bd = eval(Bd);
   
   
   for step = 1:15000
       error = x - x0;
       % 欧几里得范数也是一种k类函数
       if norm(error) >= sigma_prime * norm(x)
           x0 = x;
           u = K*x0;
           trigger_count = trigger_count + 1;
       end
       x = Ad*x + Bd*u;
       
       E = norm(error);
       ET = sigma_prime * norm(x);
       EUB = sigma * norm(x);
   
       error_buffer = [error_buffer E];
       error_trigger = [error_trigger ET];
       error_upper_bound = [error_upper_bound EUB];
       x_buffer = [x_buffer x];
       u_buffer = [u_buffer u];
       
   end
   
   %% plot
   
   figure(1)
   hold on
   plot(x_buffer', 'LineWidth', 1.5);
   plot(u_buffer, 'LineWidth', 1.5);
   legend('x1', 'x2', 'u');
   
   figure(2)
   hold on
   plot(error_buffer, 'LineWidth', 1);
   plot(error_trigger, 'LineWidth', 1.5, 'Color', 'r');
   plot(error_upper_bound, 'LineWidth', 1, 'Color', 'r');
   legend('error', 'error trigger', 'error upper bound');
   
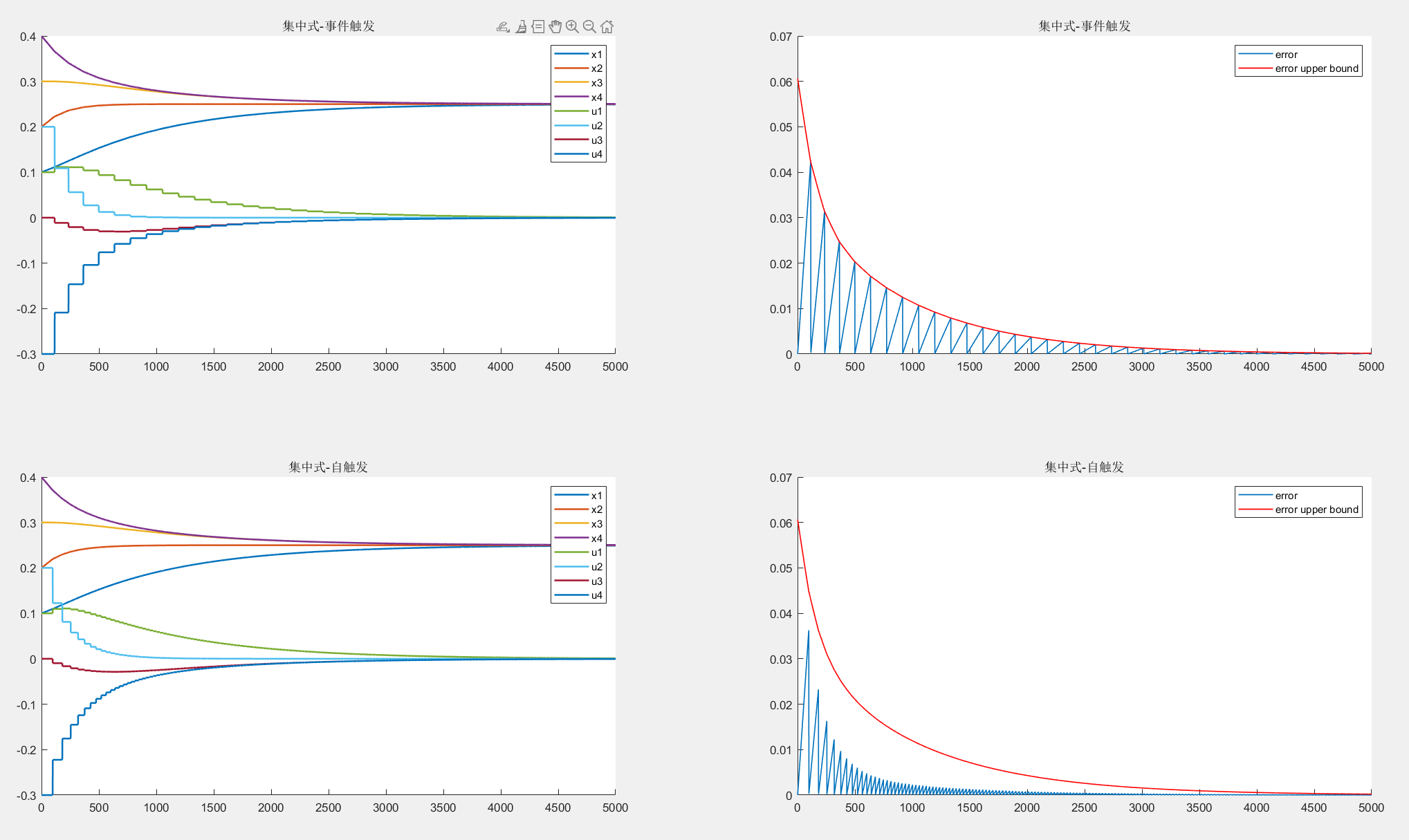
   fprintf('the system has been triggered %d times in all\n', trigger_count);

   仿真结果：

   

   

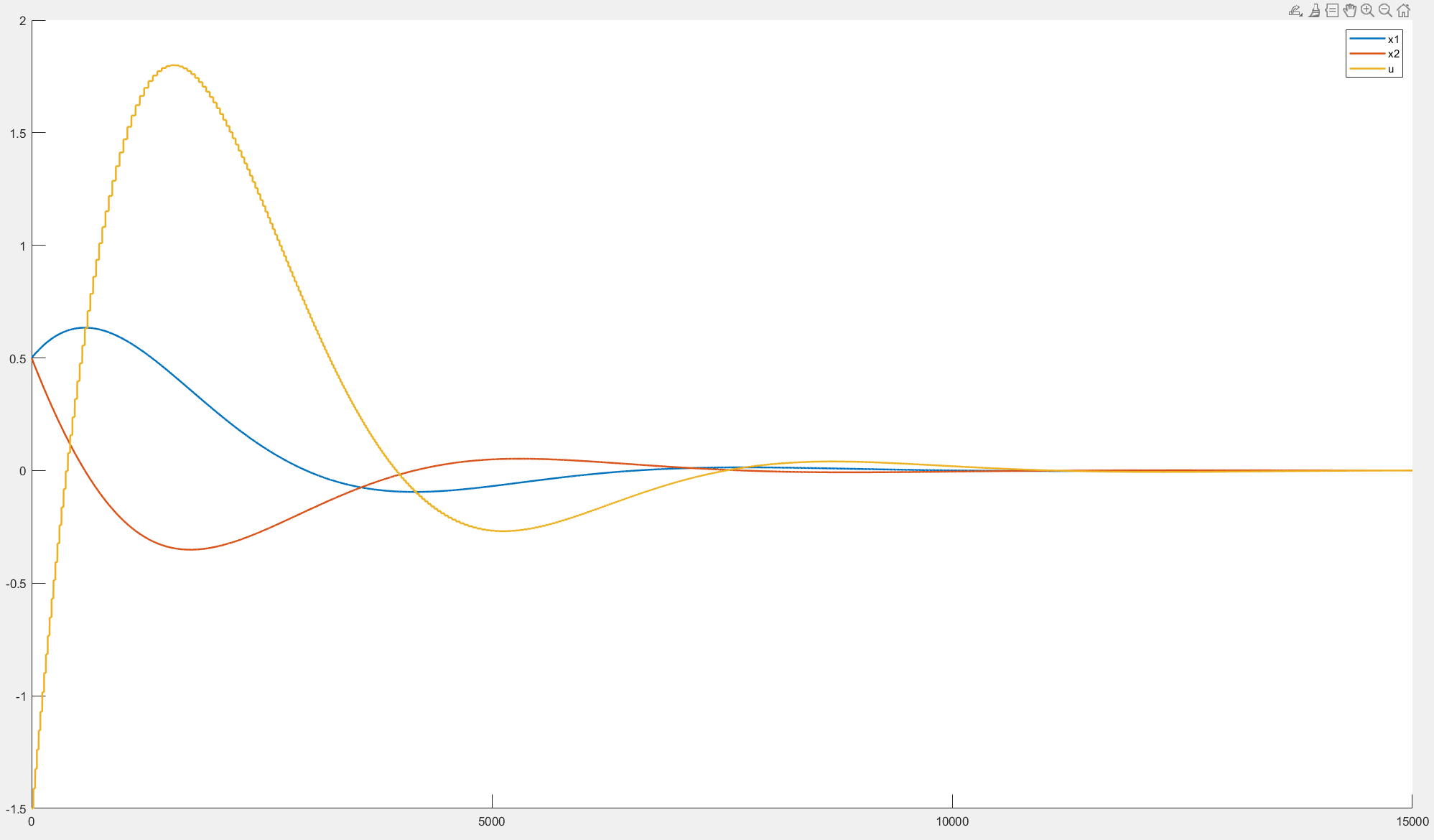
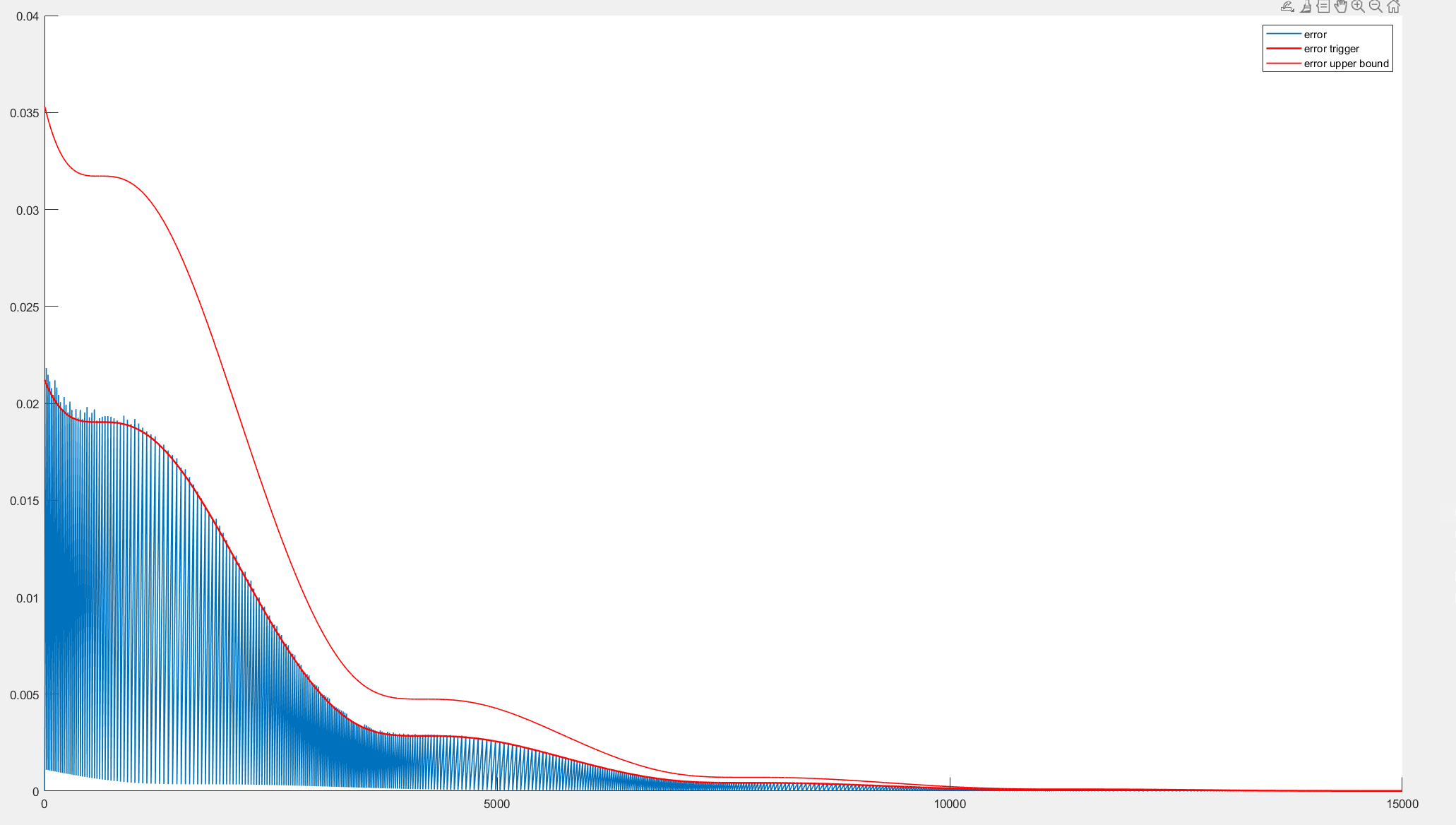
​ 可见最后的实际误差确实在由事件触发规则限制的误差之下，系统也达到了收敛状态

Paper 2：Distributed Event-Triggered Control for Multi-Agent Systems, 2012, TAC

一、motivation：

1. 上一篇文献没提”多智能体“，讲的只是一个普通的控制系统的事件触发；而这篇文章讲的MAS中的事件触发
2. 分为集中式（各个节点都知道全局信息，如拉普拉斯矩阵）和分布式（各节点只知道自己的邻居信息）
3. 给出了自触发公式：算出两次触发时间之间的上限，只要间隔不超过这个上限最后就能稳定

二、集中式事件触发

模型：单积分器 $\dot{x_i}=u_i$

控制器：$u=-Lx$

拓扑关系：无向连通图

由上述推导可知，事件触发条件为：
$$
||e||=\sigma\frac{||Lx||}{||L||}
$$

二、分布式事件触发

基本思路是每个智能体都只能获取邻居信息，无法得知全局信息（Laplace矩阵）；哐哐一通推导后得到每个智能体的事件触发条件：
$$
e_i^2=\frac{\sigma_ia(1-a|N_i|)}{N_i}z_i^2
$$

三、自触发

idea：推导出两次触发时间的间隔上界，即只要时间间隔别超过这个上界就能稳定；在自触发中，“事件”不再由误差e决定，而是取决于间隔时间
$$
\begin{aligned}\Delta&=4\sigma^4\left|(Lx(t_i))^TLLx(t_i)\right|^2\&+4\sigma^2\left|L^2x(t_i)\right|^2\cdot\left(|Lx(t_i)|^2|L|^2-\sigma^2\left|L^2x(t_i)\right|^2\right)>0.\end{aligned}
$$

$$
t_{i+1}-t_i\leq\frac{-2\sigma^2\left(Lx(t_i)\right)^TLLx(t_i)+\sqrt{\Delta}}{2\left(|Lx(t_i)|^2|L|^2-\sigma^2|L^2x(t_i)|^2\right)}
$$

四、仿真

% Distributed Event-Triggered Control for Multi-Agent Systems, 2012, TAC

clc;        
clear;      
close all;

%% system define
L = [1 -1 0 0;
    -1 3 -1 -1;
    0 -1 2 -1;
    0 -1 -1 2];

x0 = [0.1 0.2 0.3 0.4]';

sigma = 0.65;
sigma_1 = 0.55;
sigma_2 = 0.55;
sigma_3 = 0.75;
sigma_4 = 0.75;
alpha = 0.2;

dt = 0.001;
trigger_count_1 = 0;
trigger_count_2 = 0;
trigger_count_3 = 0;
trigger_count_4 = 0;


%% 集中式-事件触发
x_buffer_1 = [];
u_buffer_1 = [];
error_buffer_1 = [];
error_upper_bound_1 = [];

x = x0;         
u = -L*x0;    

B = ones(4, 1);
syms s;
Bd = int(expm(zeros(4,4)*s),0,dt)*B;
Bd = eval(Bd);

for step = 1:5000
    error = x - x0;
    E = norm(error);

    if E >= sigma * norm(L*x)/norm(L)
        x0 = x;
        u = -L*x0;
        trigger_count_1 = trigger_count_1 + 1;
    end
    x = x + Bd.*u;

    EUB = sigma * norm(L*x)/norm(L);

    error_buffer_1 = [error_buffer_1 E];
    error_upper_bound_1 = [error_upper_bound_1 EUB];
    x_buffer_1 = [x_buffer_1 x];
    u_buffer_1 = [u_buffer_1 u];
    
end


%% 集中式-自触发
x_buffer_2 = [];
u_buffer_2 = [];
error_buffer_2 = [];
error_upper_bound_2 = [];

x0 = [0.1 0.2 0.3 0.4]';
x = x0;         
u = -L*x0;  

t_now = 0;
time_upper_bound = 0;

for step = 1:5000
    error = x - x0;
    E = norm(error);
    t_next = dt*step;

    if t_next - t_now >= time_upper_bound
        x0 = x;
        u = -L*x0;
        t_now = t_next;
        time_upper_bound = 0.2*calculate_fun(sigma, L, x0);
        trigger_count_2 = trigger_count_2 + 1;
    end

    x = x + Bd.*u;

    EUB = sigma * norm(L*x)/norm(L);

    error_buffer_2 = [error_buffer_2 E];
    error_upper_bound_2 = [error_upper_bound_2 EUB];
    x_buffer_2 = [x_buffer_2 x];
    u_buffer_2 = [u_buffer_2 u];
end

figure(1)
subplot(2,2,1);
hold on
plot(x_buffer_1', 'LineWidth', 1.5);
plot(u_buffer_1', 'LineWidth', 1.5);
legend('x1', 'x2', 'x3', 'x4', 'u1', 'u2', 'u3', 'u4');
title("集中式-事件触发");

subplot(2,2,2);
hold on
plot(error_buffer_1, 'LineWidth', 1);
plot(error_upper_bound_1, 'LineWidth', 1, 'Color', 'r');
legend('error', 'error upper bound');
title("集中式-事件触发");

fprintf('1： triggered %d times in all\n', trigger_count_1);

subplot(2,2,3);
hold on
plot(x_buffer_2', 'LineWidth', 1.5);
plot(u_buffer_2', 'LineWidth', 1.5);
legend('x1', 'x2', 'x3', 'x4', 'u1', 'u2', 'u3', 'u4');
title("集中式-自触发");

subplot(2,2,4);
hold on
plot(error_buffer_2, 'LineWidth', 1);
plot(error_upper_bound_2, 'LineWidth', 1, 'Color', 'r');
legend('error', 'error upper bound');
title("集中式-自触发");

fprintf('2： triggered %d times in all\n', trigger_count_2);