论文学习:A survey of distributed optimization
一些参考:
Distributed Optimization Algorithms
分布式优化(Distributed Optimization)前置介绍和一些思考:
现实背景:最优编队控制问题,即既要求实现传统的位置consensus以形成特定编队,也要在某些指标(变换队形时的总移动距离、能耗balabala)达到最优。
$$
每个智能体的代价函数:f_i(\phi_i)=c_i|\phi_i-\phi_i(0)|_2^2
$$
$$
总的的代价函数:f(\phi)=\sum_{i=1}^Nc_i|{\phi_i}-\phi_i(0)|_2^2
$$
比较:
-
和传统consensus:
传统consensus不要求达到最优;
相当于是在传统consensus的基础上多加了一道最优的考虑;
拓扑结构不影响分布式优化的具体收敛值
-
和普通优化:
考虑拓扑信息,不是分别计算每个个体的最优然后相加;
最终各agent的收敛值是一致的,而如果单考虑个体目标函数的话那收敛值肯定不一样
Q1:代价函数的自变量一定要是智能体的状态 xi 吗?
A1:对于经典分布式优化问题来说一般是这样,但也可改变自变量得到其它形式的问题。如唐于涛嵌入式作品中研究的就是最优输出一致性问题(optimal output consensus),自变量是输出值y —— 当然,本质上还是个分布式优化问题,用的还是那些优化算法($f(y)=\sum_{i=1}^{N}f_{i}(y)$)

Q2:每个智能体的$f_i(x_i)$最终的收敛值是相同的吗?
A2:严格来说不是相同,而是达成consensus;至于这个consensus是完全相等(一般的分布式优化问题)还是差了一个固定常数(编队问题)就取决于问题本身了,也就是说,分布式优化中的consensus部分和传统consensus是一回事。
Q3:分布式优化的最终结果和普通consensus结果是一样的吗?
A3:没有直接关系,看优化部分长啥样。分布式优化=普通consensus(群体交互) + 普通优化(个体计算),其中consensus部分的结果就是常规一致性算法得到的结果,它保证了各agent的收敛值是相同的(或者差一个常数);而优化部分决定了这个收敛值具体是多少。
如下面那个DGD的仿真中,目标函数是$x^2$时,收敛值为0;为$(x-1)^2$收敛值就为1了(当然,这是能收敛的情况,拓扑图中没有生成树时肯定就收敛不到这个值了;有生成树时拓扑不同收敛速度也会不同)
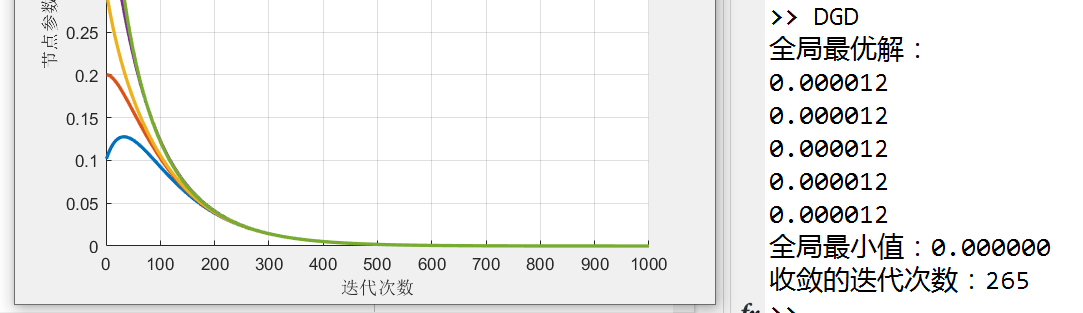
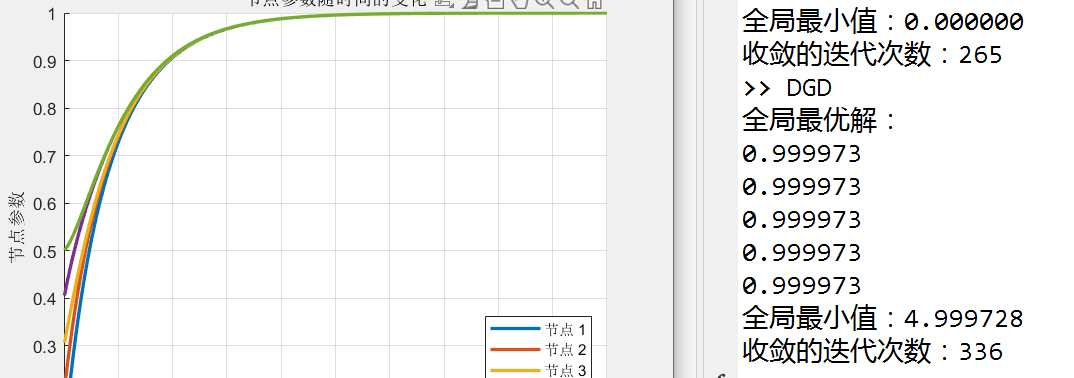
Q4:普通consensus的拓扑影响最终的收敛值,而分布式优化的拓扑不影响,对吗?
A4:假设大前提是拓扑中存在生成树,那么普通consensus的最终收敛值确实取决于拓扑结构,因为从consensus算法就可以看出来,算法本身只保证各节点值达到一致,而不保证这个值具体是多少,拓扑不同时,能分享的信息程度不同,收敛值自然就不一样。
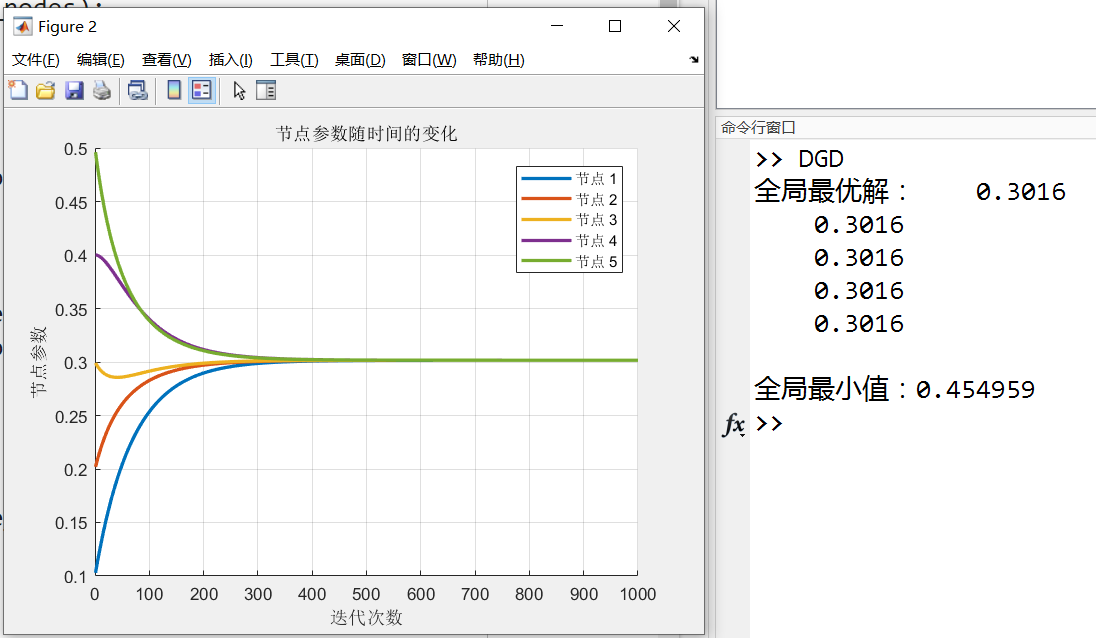
无需太多解释,为无向图完全连通时,最终各节点值趋于全局的平均值
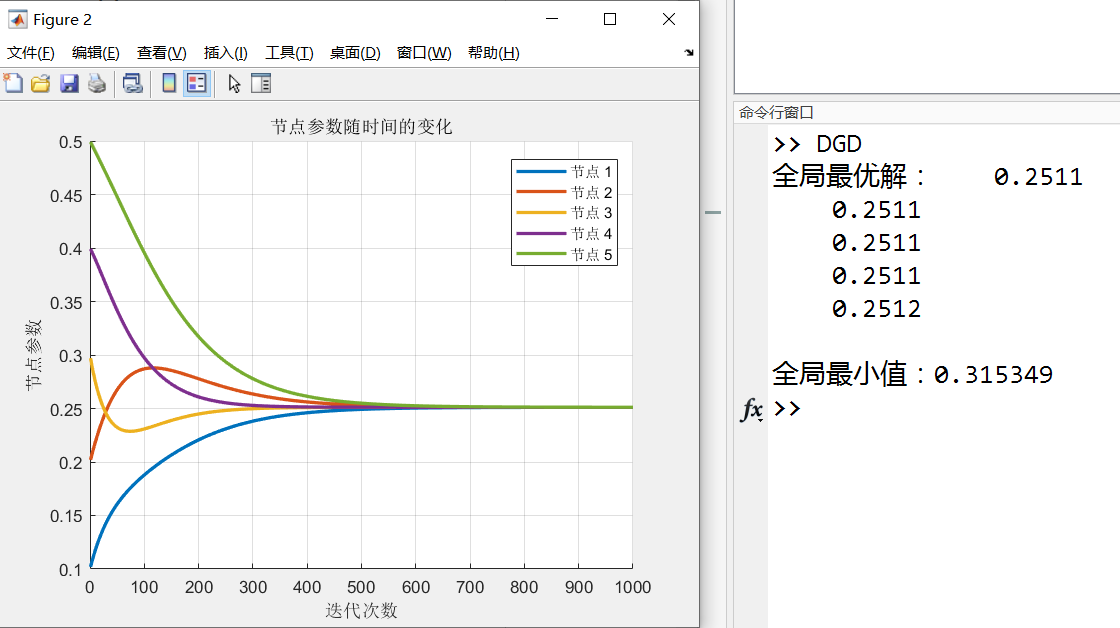
为有向图时,因为不是各节点之间都还能“均匀地”通信,所以结果也不再是全局平均
而对于分布式优化来说,可以把收敛过程拆成独立的两部分来理解:
第一部分,拓扑起作用,经典consensus保证了各agent值一致(不管是全局平均值还是加权平均值,反正是一致的);
第二部分,拓扑不起作用,各自梯度下降,达到目标函数的(局部)最优点。
也就是说,在普通consensus中,由于拓扑不同,可能导致”还没来得及收敛到全局平均,大家的值就相同了,那好吧,只能停下来了“;而在分布式优化中,就算达到了该拓扑下的加权平均,只要梯度不为0、没到目标函数的最优点,那就还会拖着$x_i$继续变换,直至达到最优且一致。
所以分布式优化的拓扑仅影响收敛速度和稳定性,不影响具体收敛值。
A survey of distributed optimization, 2019, Annual Reviews in Control
一、introduction
- 分布式优化
$$
\min_{x\in\mathbb{R}^n}\sum_{i=1}^Nf_i(x),
$$
二、离散时间分布式优化算法
-
递减步长(diminishing step-sizes)
DGD: Distributed Gradient Descent
$$
x_i(k+1)=\sum_{j=1}^Nw_{ij}(k)x_j(k)-\alpha(k)s_i(k),
$$
其中$w_{ij}(k)$是边的权重,$s_i(k)$是局部函数$f_i(x)$的(次)梯度,$\alpha(k)>0$是递减的步长,其满足:
$$
\sum_{k=0}^\infty\alpha\left(k\right)=\infty,\sum_{k=0}^\infty\alpha^2(k)<\infty,
$$$$
\alpha\left(k\right)\leq\alpha\left(s\right)\mathrm{~for~all~}k>s\geq0.
$$💡 PS. 注意,原文中假设了$\sum_{j=1}^m w_{ij}(k)=1$,即边的权重是均值归一化了的,所以上面的公式中的consensus部分和常见的一致性算法$x_i(k+1)=x_i(k)+u,\quad u=\sum a_{ij}(x_j-x_i)$其实是一模一样的(推导略)
DGD算法本质上是将优化过程分成了两部分:一部分是consensus,即利用Weight matrix将连通节点的信息做一个沟通;另一部分就是传统的梯度下降,这里的梯度下降是针对每一个local节点。而DGD有一个显著的缺点:如果DGD当中的步长选择常数的话,那么会得到inexact convergence;而如果选择逐渐趋于零的步长(diminishing step size),那么虽然可以得到exact convergence, 但是会造成较慢的收敛速度,这在实际应用当中是一个棘手的问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89% DGD仿真
num_nodes = 5; % 节点数量
% 有向图
adjacency_matrix_dir = [ 1 0 -1 0 0;
-1 2 0 0 -1;
-1 -1 2 0 0;
0 0 -1 1 0;
0 0 0 -1 1];
% 无向图
adjacency_matrix_undir = [ 2 -1 -1 0 0;
-1 2 0 0 -1;
-1 0 2 -1 0;
0 0 -1 2 -1;
0 -1 0 -1 2];
% 初始化节点参数和本地梯度
%node_params = rand(num_nodes, 1); % 初始参数
node_params = [0.1 0.2 0.3 0.4 0.5]';
local_gradients = 0;
% 设置全局目标函数(示例中为简单的平方和)
global_objective = @(x) sum(x.^2);
num_iterations = 1000;
consensus_ratio = 0.01;
fixed_step_size = 0.005;
diminish_step_size = 0.005;
% 创建用于存储可视化数据的数组
param_history = zeros(num_iterations, num_nodes);
iteration_converge = 0;
difference = 0;
for iteration = 1:num_iterations
for node = 1:num_nodes
local_gradients = 2 * node_params(node);
% 一致性部分
for neighbor = 1:num_nodes
if adjacency_matrix_undir(node, neighbor) == -1
node_params(node) = node_params(node) - consensus_ratio * (node_params(node) - node_params(neighbor));
end
end
% 梯度下降部分
diminish_step_size = -0.0045/1000*iteration + 0.005;
node_params(node) = node_params(node) - fixed_step_size * local_gradients;
end
% 存储参数历史
param_history(iteration, :) = node_params;
% 记录收敛所需迭代次数
for node = 2:num_nodes
difference = difference + abs(node_params(1)-node_params(node));
end
if iteration_converge == 0 && difference < 0.001
iteration_converge = iteration;
end
difference = 0;
end
% 输出最终的全局最优解
global_minimizer = node_params;
global_minimum = global_objective(global_minimizer);
fprintf('全局最优解:\n');
fprintf('%2f\n', global_minimizer);
fprintf('全局最小值:%f\n', global_minimum);
fprintf('收敛的迭代次数:%d\n', iteration_converge);
figure;
hold on;
for node = 1:num_nodes
plot(1:num_iterations, param_history(:, node), 'LineWidth', 2, 'DisplayName', sprintf('节点 %d', node));
end
xlabel('迭代次数');
ylabel('节点参数');
title('节点参数随时间的变化');
legend('Location', 'Best');
grid on;
hold off;仿真结果:
见开头Q3
-
固定步长(fixed step-sizes)
EXTRA: Exact first-order algorithm
第一步:
$$
x_i(1)=\sum_{j=1}^Nw_{ij}x_j(0)-\alpha\nabla f_i(x_i(0)),
$$
其中$\alpha>0$是固定步长
第二步:
$$
\begin{aligned}x_i(k+2)&=x_i(k+1)+\sum_{j=1}^Nw_{ij}x_j(k+1)-\sum_{j=1}^N\tilde{w}_{ij}x_j(k)-\alpha\left(\nabla f_i(x_i(k+1))-\nabla f_i(x_i(k))\right),\mathrm{~}k=0,\mathrm{~}1,\ldots,\end{aligned}
$$
相较于DGD算法,EXTRA用到了前两步的梯度信息,文献表明,EXTRA可以看作是具有误差校正项的DGD
DIGing: distributed inexact gradient method and the gradient tracking
公式如下:
$$
x_i(k+1) =\sum_{j=1}^Nw_{ij}x_j(k)-\alpha y_i(k),
$$
$$
y_{i}(k+1) =\sum_{i=1}^Nw_{ij}y_j(k)+\nabla f_i(x_i(k+1))-\nabla f_i(x_i(k))
$$
Distributed PI algorithm
公式如下:
$$
x_i(k+1)=x_i(k)-v_i(k)-\alpha\nabla f_i(x_i(k))-\beta\sum_{j\in\mathcal{N}i}a{ij}(x_i(k)-x_j(k)),
$$
$$
\nu_i(k+1) =v_i(k)+\alpha\beta\sum_{j\in\mathcal{N}i}a{ij}(x_i(k)-x_j(k))
$$
-
一阶梯度算法
Distributed PI algorithm
公式如下:
$$
\dot{x}i(t) =\sum{j=1}^Na_{ij}(x_j(t)-x_i(t))+\sum_{j=1}^Na_{ij}(\nu_j(t)-\nu_i(t))-\nabla f_i(x_i(t)),
$$
$$
\dot{\nu}i(t) =\sum{j=1}^Na_{ij}(x_i(t)-x_j(t))
$$
-
二阶梯度算法
Zero-Gradient-Sum Algorithm
公式如下:
$$
\dot{x}i(t)=\gamma\left(\nabla^2f_i(x_i(t))\right)^{-1}\sum{j\in\mathcal{N}i}a{ij}(x_j(t)-x_i(t))
$$
四、拓展场景中的分布式优化算法
- 有向图
Distributed Push-Sum Based Algorithm(离散时间)
大部分现有的有向图离散时间分布式算法都是基于推和
-
时延
-
随机拓扑
-
事件触发机制(精读!)
-
有限时间收敛