基于CPU SIMD和winograd的卷积计算加速技术

参考：

AI算法基础：Winograd算法原理

卷积神经网络中的Winograd快速卷积算法

从TensorRT看INT8量化原理

MegEngine Inference 卷积优化之 Im2col 和 winograd 优化

一、introduction

  1. motivation

    网络训练耗时过大，卷积层是CNN前向推理计算的主要计算瓶颈。在广泛使用的CNN模型中，卷积层的运算量可占到95%以上。

    ​

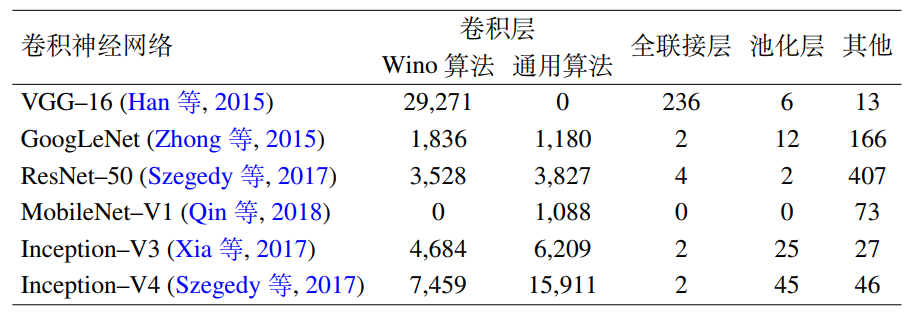
  2. 直接卷积算法

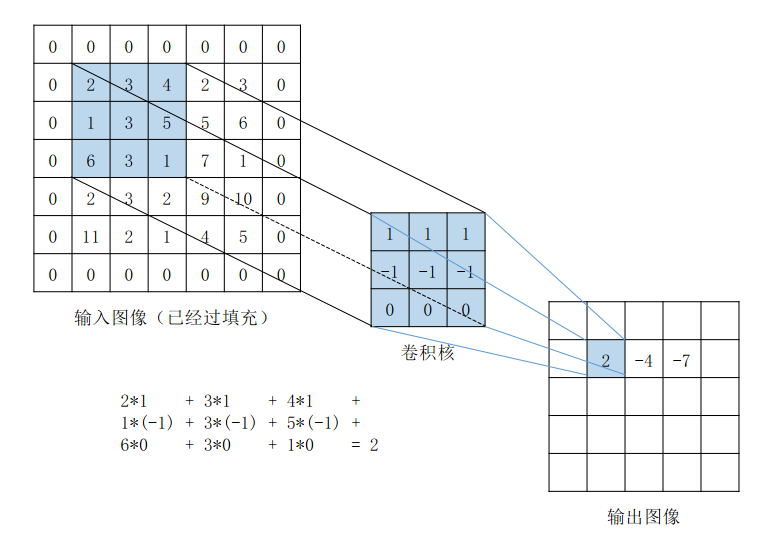
​ 为啥直接卷积算法容易拖慢性能呢？

  • 最内层的乘加语句（伪代码的第9行）无法向量化，因为无法在卷积核上连续读入一个向量寄存器长度的数据
  • 会重复读数据，类似于递归计算斐波那契数列，缺乏记忆化过程

二、卷积加速算法

  1. 介绍

    Winograd算法起源于1980年，作者Shmuel Winograd 在文章《On multiplication of polynomials modulo a polynomial》中提出的减少FIR滤波器计算量的一个算法。他指出，对于输出个数为m，参数个数为r的FIR滤波器，不需要m×r次乘法计算，而只需要u(F(m,r))=m+r−1次乘法计算即可。
    后来，有人发现此算法可以用来优化加速CNN网络的卷积计算《Fast Algorithms for Convolutional Neural Networks》，从此Winograd算法被广泛应用于各推理框架中。

  2. 1D winograd算法

    以1维卷积$F(2, 3)$为例，输入信号$d=[d_0,d_1,d_2,d_3]^T$，卷积核$g=[g_0,g_1,g_2]^T$，那么卷积可以写成下列矩阵乘法形式：
    $$
    F(2,3)=\begin{bmatrix}d_0&d_1&d_2\d_1&d_2&d_3\end{bmatrix} \begin{bmatrix}g_0\g_1\g_2\end{bmatrix}=\begin{bmatrix}r_0\r_1\end{bmatrix}
    $$
    如果这个计算过程使用普通的矩阵乘法，一共需要 6 次乘法 + 4次加法：
    $$
    r_0=d_0g_0+d_1g_1+d_2*g_2
    $$
    但是，我们仔细观察一下，卷积运算中输入信号转换得到的矩阵不是任意矩阵，其有规律的分布着大量的重复元素，例如$d_1$和$d_2$。Winograd做了如下变换：

    $$
    F(2,3)=\begin{bmatrix}d_0&d_1&d_2\d_1&d_2&d_3\end{bmatrix}\begin{bmatrix}g_0\g_1\g_2\end{bmatrix}=\begin{bmatrix}m_1+m_2+m_3\m_2-m_3-m_4\end{bmatrix}
    $$
    其中，

$$
\begin{aligned}m_1&=(d_0-d_2)g_0&m_2=(d_1+d_2)\frac{g_0+g_1+g_2}{2}\m_4&=(d_1-d_3)g_2&m_3=(d_2-d_1)\frac{g_0-g_1+g_2}{2}\end{aligned}
$$

​ 在CNN的推理阶段，卷积核上的元素是固定的，所以上式中和 g 相关的式子可以提前在模型初始化阶段算好，整个推理阶段只用计算一次，因此可以忽略。所以这里一共需要 4次乘法 + 8次加法。

​ 上面其实就是1D的Winograd算法，我们将上面的计算过程写成矩阵的形式：
$$
Y=A^T[(Gg)\odot(B^Td)]
$$
​ 其中，

  • $\odot$表示element-wise multiplication（Hadamard product），即对应位置相乘操作；

  • $g$ 表示卷积核；

  • $d$ 表示输入特征图；

  • $G$ 表示卷积核变换矩阵，尺寸为$(u+k−1) × k$；

  • $B^T$ 表示输入变换矩阵，尺寸为$(u+k−1) × k$；

  • $A^T$ 表示输出变换矩阵，尺寸为$(u+k−1) × u$；

  • $u$ 表示输出尺寸，$k$表示卷积核尺寸，$su=(u+k−1)$表示输入尺寸

    各矩阵具体值如下：

$$
B^T=\begin{bmatrix}1&0&-1&0\0&1&1&0\0&-1&1&0\0&1&0&-1\end{bmatrix}
$$

$$
G=\begin{bmatrix}1&0&0\\frac12&\frac12&\frac12\\frac12&-\frac12&\frac12\0&0&1\end{bmatrix}
$$

$$
g=\begin{bmatrix}{g_{0}}&{g_{1}}&{g_{2}}\end{bmatrix}^{T}
$$

$$
d=\begin{bmatrix}d_0&&d_1&&d_2&&d_3\end{bmatrix}^T
$$

​ $G, B^T, A^T$三个变换矩阵的推导原理及过程可以通过github工具wincnn计算：

计算F(2,3)的变换矩阵

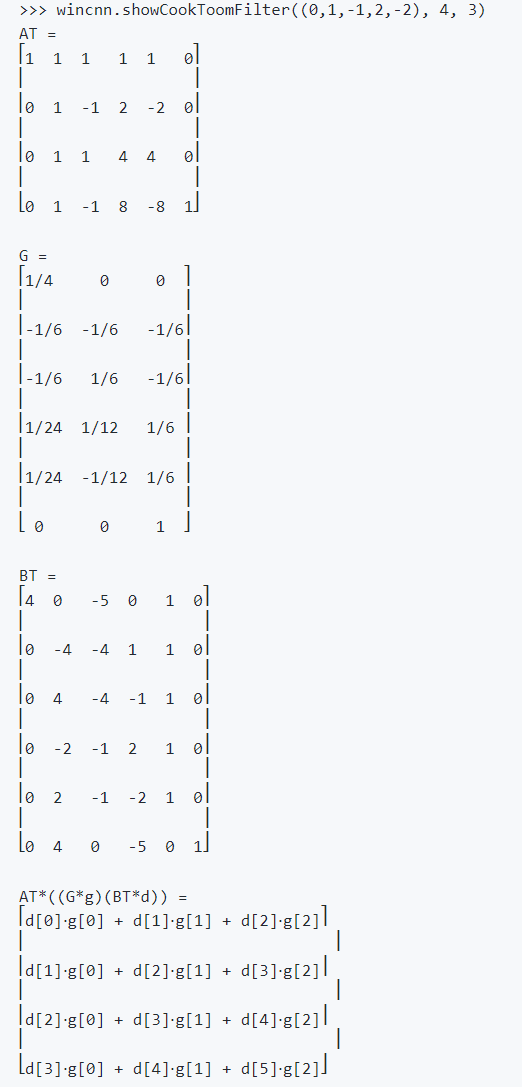
计算F(4,3)的变换矩阵

  1. 关于乘法和加法的计算量讨论

    为啥从经典卷积的6次乘法 + 4次加法，到winograd的4次乘法 + 8次加法就认为是耗时更少捏？

    下面是一个经典的二进制全加器，输入A和B以及进位Cin，输出Sum和进位输出Co

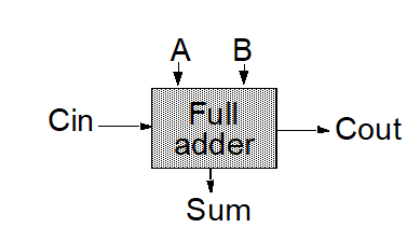
    二进制全加器

    而实现乘法常用的方法是类似于手工计算乘法的方式：

​

​ 对应的硬件结构就是阵列乘法器，计算思路是生成部分积，累加部分积和最终相加

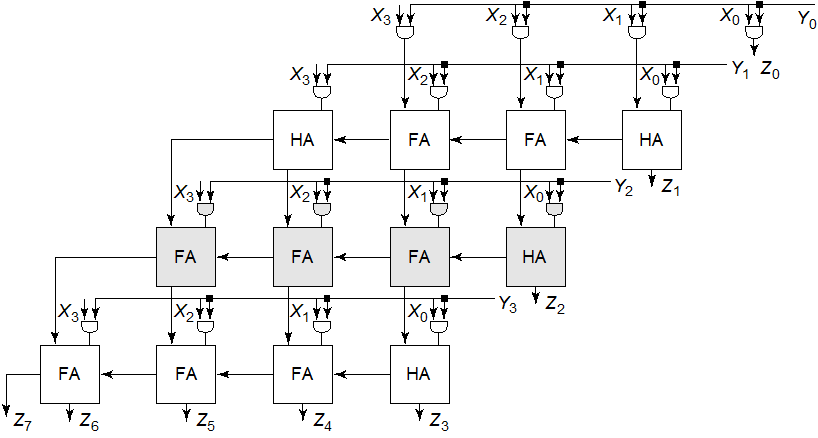
​ 阵列乘法器

​ 可见乘法器无论是元件面积还是计算耗时都大于加法器

​ 但是，上述经典理解适用于现代代码优化吗？

​ 对于下面这样一段代码：

1
2
3
4
5
6
7
int main()
{
    int sum;
    sum = 10;
    sum *= 3;
    return sum;
}

​ 使用gcc -S -masm=intel得到汇编语句：

​

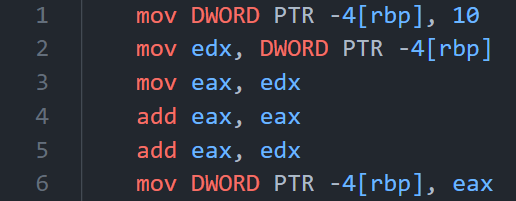
​ 可以看到，sum*=3被拆成了1条mov和两条add，没有用乘法

​ 如果是sum*=2的话，则为：

​

​ 这下连add都省了，直接sal算术左移一位，即sum<<=1

​ 上述情况还都只是-O0编译优化，如果我们开到-O3

1
2
3
4
5
6
7
8
int main()
{
    int i, sum = 0;
    for(i=0; i<10; i++) {
        sum += 2;
    }
    return sum;
}

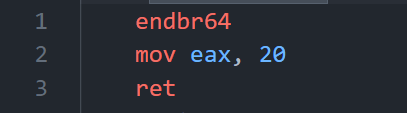
非常有意思，循环直接被优化掉了

另外，在现代cpu的分支预测、SIMD向量运算的作用下，数值计算的耗时绝不仅仅是“乘法比加法慢”这么简单，这给我们的启发是，只要写出可读性足够好的代码就行，不要自作聪明地去人为优化，编译器会帮你做好这件事的，premature optimization is the root of evil

  1. 2D winograd算法

将$F(2,3)$扩展到$F(2×2,3×3)$:

​ 我们可以看到上面切分的每一块其实际就是1D的卷积操作，写成矩阵块形式：

​ 上图中最后得到$M_0…M_3$的操作为4次矩阵加法以及4次矩阵乘法，由$M_0…M_3$得到$[R0,R1]^T$为4次矩阵 加法，同样$W$矩阵的转换的计算量忽略不计。

  • $K_{0…3}$之间的4次矩阵加法， 每次实际为4次加法（注意不要被上面扩展后的$K$矩阵划分的小方块中6个元素所迷惑，其中有重复的元素），共4×4=16次加法；
  • 4次矩阵乘法可以转换为4次 1D Winograd 来计算，每次 1D Winograd 计算中有4次乘法，8次加法，共4×4=16次乘法，4×8=32次加法；
  • 最后$M_0…M_3$之间的4次矩阵加法，由于$M$矩阵的尺寸为2×1，所以共4×2=8次加法；综上，$F(2×2,3×3)$的Winograd算法共 16次乘法和56次加法，如果使用常规卷积运算，则需要 36次乘法和32次加法

​ 上面的计算过程写成矩阵的形式如下:
$$
Y=A^T[[GgG^T]\odot[B^TdB]]A
$$

  1. 1D到2D的公式推导

    约定：大写字母或小写字母加上箭头均代表矩阵或向量，$K_0$与$\overrightarrow{d_0}$均表示输入矩阵的第一行，$W_0$与$\overrightarrow{k_0}$均表示卷积核的第一行

    这里沿用2D Winograd推导中的字母表示，最后会转为1D Winograd推导中的字母表示

​ 首先对上述公式进行重排，输出为2×2矩阵：
$$
[R_0,R_1]=[M_0+M_1+M_2,M_1-M_2-M_3]\=[M_0,M_1,M_2,M_3]\begin{bmatrix}1&0\1&1\1&-1\0&-1\end{bmatrix}=[M_0,M_1,M_2,M_3]A
$$
​ 结合上面计算代入$M_n$得下式：
$$
\begin{aligned}
&[R_0,R_1]= \
&\left[A^{T}[(GW_{0})\odot(B^{T}(K_{0}-K_{2}))],A^{T}[(G\frac{W_{0}+W_{1}+W_{2}}{2})\odot(B^{T}(K_{1}+K_{2}))],\right. \
&A^{T}[(G\frac{W_{0}-W_{1}+W_{2}}{2})\odot(B^{T}(K_{2}-K_{1}))],A^{T}[(GW_{2})\odot(B^{T}(K_{1}-K_{3}))]\Biggr]A \
&=A^T\bigg[[(GW_0)\odot(B^T(K_0-K_2))],[(G\frac{W_0+W_1+W_2}{2})\odot(B^T(K_1+K_2))], \
&[(G\frac{W_0-W_1+W_2}2)\odot(B^T(K_2-K_1))],[(GW_2)\odot(B^T(K_1-K_3))]\Biggr]A
\end{aligned}
$$
​ 由于hadamard product（$\odot$）和concat（,）操作可以交换而不影响结果，因此：
$$
\begin{aligned}
&[R_0,R_1]= \
&A^T\bigg[(G[W_0,\frac{W_0+W_1+W_2}{2},\frac{W_0-W_1+W_2}{2},W_2])\odot\big(B^T[K_0-K_2,K_1+K_2,K_2-K_1,K_1-K_3]\big)\bigg]A \
&=A^T\bigg[(G[W_0,W_1,W_2]\begin{bmatrix}1&\frac{1}{2}&\frac{1}{2}&0\0&\frac{1}{2}&-\frac{1}{2}&0\0&\frac{1}{2}&\frac{1}{2}&1\end{bmatrix})\odot(B^T[K_0,K_1,K_2,K_3]\begin{bmatrix}1&0&0&0\0&1&-1&1\-1&1&1&0\0&0&0&-1\end{bmatrix})\bigg]A \
&=A^T\bigg[(G[\overrightarrow{k_0},\overrightarrow{k_1},\overrightarrow{k_2}]G^T)\odot(B^T[\overrightarrow{d_0},\overrightarrow{d_1},\overrightarrow{d_2},\overrightarrow{d_3}]B)\bigg]A \
&=A^T[(GKG^T)\odot(B^TDB)]A
\end{aligned}
$$

  1. 总结

    Winograd算法可以分为4个步骤：

    1. 初始化期间完成卷积核的变换weightTransform，即：$GKG^T$
    1. 运行期间完成输入数据的变换sourceTransform，即：$B^TDB$
    1. 运行期间完成输入数据与权重的MatMul，即：$(GKG^T)\odot(B^TDB)$
    1. 运行期间完成输出数据的变换dstTransform，即：$A^T[(GKG^T)\odot(B^TDB)]A$
自己事情靠自己
#SIMD #体系结构 #AI边缘计算
基于CPU SIMD和winograd的卷积计算加速技术
https://qlhhahaha.github.io/2023/09/15/winograd卷积加速算法/
作者
qlhhahaha
发布于
2023年9月15日
许可协议